RNN은 순서 변화에 따른 의미의 변화를 찾아낸다.
컴퓨터 비전에서는 CNN(합성곱 신경망)이 유용하게 쓰이지만, NLP의 경우 RNN이 유용하다.
CNN은 이미지의 패턴을 찾아내는 데 있어 좋은 성능을 보인다. 하지만 이미지와 달리 언어의 경우, '순서'라는 성질이 중요하다.
Example
① I love google.
② I google love.
문장 ①의 경우, 나는 구글을 사랑한다는 의미이지만, 문장 ②는 나는 love를 구글에 검색해보았다는 의미를 지닌 문장이 된다.
같은 단어들로 구성된 문장이라 할 지라도 단어가 배열된 '순서'에 따라 각 단어의 역할이 바뀌고, 문장의 뜻이 달라지는 것이다. 그렇기에 NLP에서는 '순서'를 내포하는 순환 신경망(RNN)을 이용한다.
RNN이란
0과 1로만 구성된 수열이 있다고 가정했을 때, 수열은 01101010100...과 같은 형태를 띈다. 이러한 수열의 원소들 중 1의 개수를 세어봤을 때 홀수와 짝수를 분류하는 문제를 가정하자.
가장 쉬운 방식은 첫 번째부터 마지막 원소까지 차례로 살펴보면서 1의 개수를 세고, 홀수인지 짝수인지 판별하여 분류하게 될 것이다.
또 다른 방식은 첫 번째 원소부터 마지막 원소까지 차례로 훑어가면서 1을 세는 대신, 홀짝을 바꾸는 것이다. 맨 처음에는 0개일 테니 짝으로 시작해서 1개가 될 때 홀로, 2개가 될 때 짝으로, 이런 식으로 개수는 세는 대신, 홀 짝을 번갈아 가면서 여부만 판별한다.
위의 제시한 방법을 통해 첫 번째 원소부터 차례로 훑어서 현재 t번째 원소를 살펴보고 있다고 한다면, 전자이 경우 t-1번째 원소까지 1의 개수, 후자의 경우 t-1번째 원소까지의 홀짝 여부를 알고 있어야 할 것이다. 즉, 위 분류 문제를 해결하기 위해서는 일종의 '저장 장치'가 필요하다.
이를 위하여 RNN에는 Hidden state라는 저장 장치가 존재한다.
RNN 구축
앞선 분류 방식 중 좀 더 효율적인 두 번째 방식을 채택한다면 Hidden state는 이전 원소까지의 홀짝 여부를 지칭할 것이다.
Hidden state는 짝이면 [1, 0], 홀이면 [0, 1]과 같이 2차원의 배열로 표현된다.

x_t는 입력, y_t는 출력, h_t는 hidden state를 의미한다. 입력으로 수열의 첫 번째 원소부터 마지막 원소까지 차례로 넣게 된다. 각 스텝마다 입력 값, 이전 스템의 hidden state를 받아서 새로운 hidden state와 출력 값을 산출하게 된다.
위에서 가정한 분류 문제를 가지고 RNN 구조를 설명하면, x_0에 수열의 첫 번째 원소를 넣어주고, 처음에 짝으로 시작하므로 h_-1에는 짝을 나타내는 [1, 0]을 집어넣는다. 이를 가지고 첫 단계에서는 첫 원소까지의 홀짝 여부를 산출하고 y_0과 h_0에 해당되는 값을 넣어준다. 이어 h_0와 두 번재 원소를 지칭하는 x_1을 두 번째 단계에 입력을 받고 그에 맞는 출력 값과 hidden state를 산출하는
순환적 구조를 보인다.
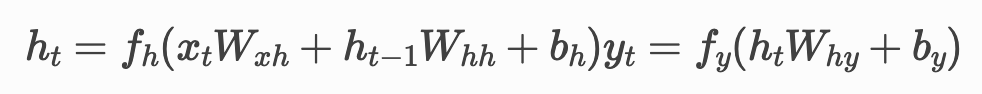
· h_t는 t번째 단계의 hidden state이다.
· x_t는 수열의 (t+1)번째 원소이다. (t = 0, 1, 2, 3, ..., T-1. T는 수열의 길이)
· W와 b는 각 밀집 층의 weight와 bias, 학습을 통해 변화하게 될 value이다.
· hidden state인 h_t는 입력 값 x_t와 이전 hidden state인 h_t-1을 결합하고 활성화 함수 f_h를 적용한 값이다.
· y_t는 hidden state h_t에 활성화 함수 f_y를 적용한 출력값이다.
· y_T-1은 수열의 홀짝 여부를 나타내는 최종 출력값이다.
위 식이 순환적으로 돌아가면서, 총 T개의 출력값과 hidden state들이 생성된다.
Transforming to be Linear
(t번째 항까지 짝 여부) = ((t-1)번째 항까지 짝 여부)^(t번째 항)
( ^은 xor 연산자)
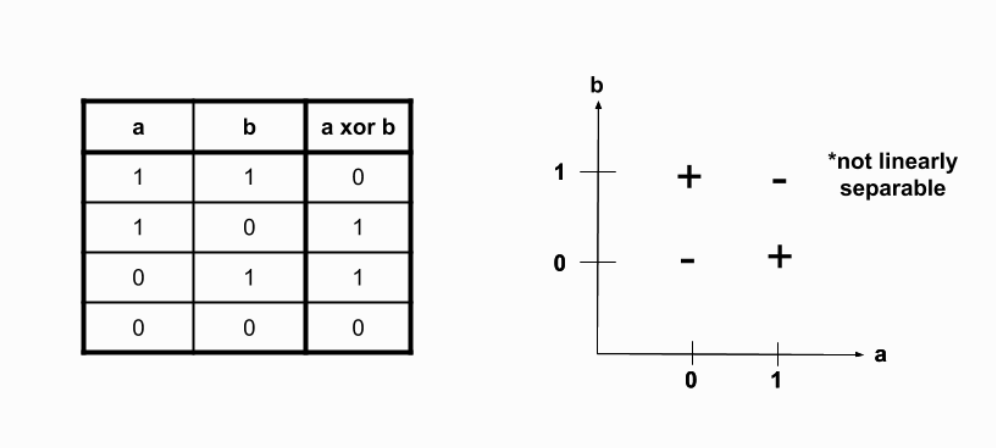
위의 RNN 예시에서 t번째 항까지 짝 여부는 짝일 경우 1, 아닐 경우 0의 값으로 표현된다고 가정한다면,
만일 (t-1)번째 항까지 짝수이고, t번째 항의 값이 1이라면 t번째 항까지는 홀수가 될 것이다. 그리고 (t-1)번째 항까지 홀수이고, t번째 항의 값이 1이라면 t번째 항까지 짝수가 될 것이다. 이때, 전자는 1과 1의 xor 값이므로 0이고, 후자는 0과 1의 xor 값이므로 1이다.
이와 같은 방식으로 입력 값과 hidden state에 xor 연산자를 한 번 적용함으로써 출력 값을 산출해낼 수 있는 것이다.
xor 연산자는 선형적이지 않다. 위 이미지를 보더라도 그렇지 않다는 것을 직관적으로 파악할 수 있다.
그렇다면, 이를 선형적인 함수들의 함성으로 표현해볼 수 있다. 바로 or와 nand 연산자로 xor을 표현해 볼 수 있을 것이다.
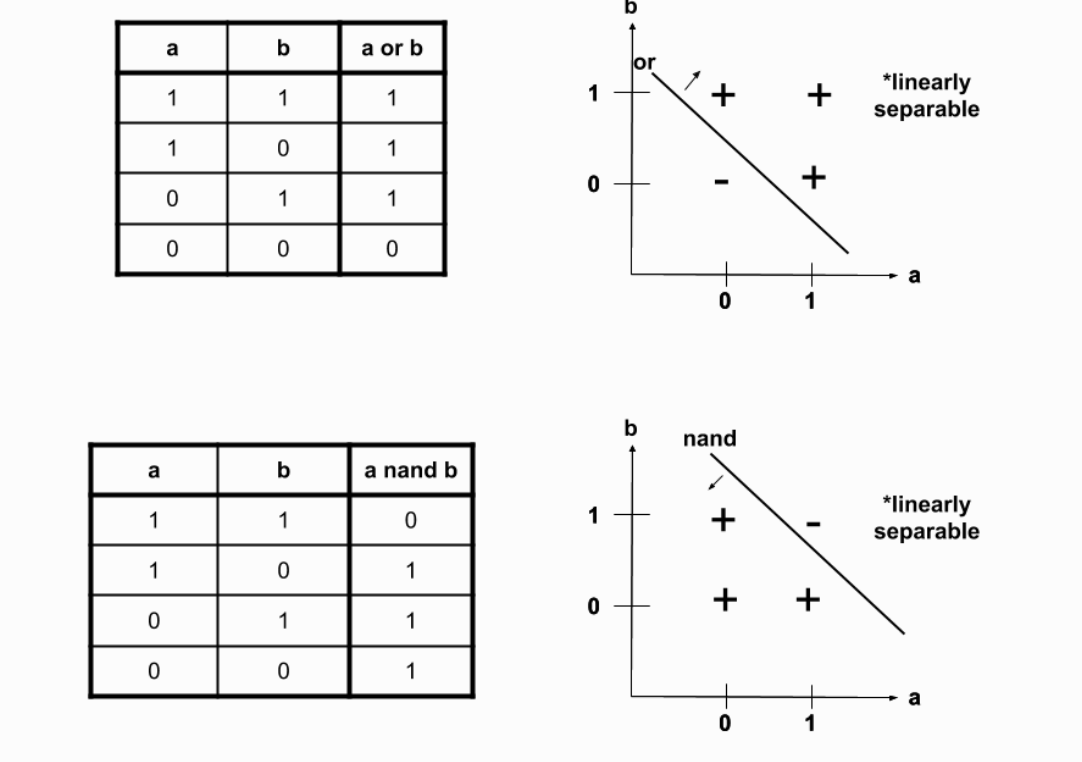
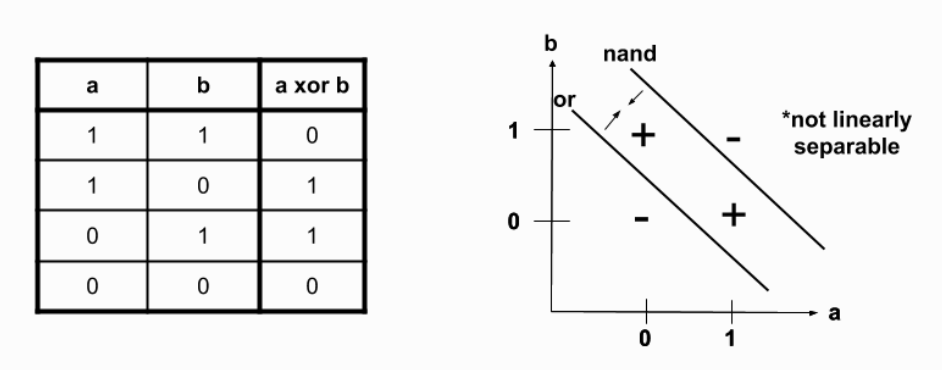
위 이미지처럼 xor는 or와 nand의 교집합이다. 즉, xor는 (nand && or) 로 표현 가능하다.

각 밀집 층은 일반적으로 여러 차례의 행렬 곲을 진행하고 활성화 함수를 적용하는 형태이다. 활성화 함수의 비선형성이 빛을 발하기 위해서는 활성화 함수에 입력되는 값들의 선형성이 보장되어야 하기 때문이다.
Backpropagation
지금까지는 순전파를 통한 최종 결과 값 도달이 목표였다. 이제 출력된 값들을 바탕으로 역전파를 활용해 각 step 별 gradient를 계산한다.
RNN의 경우 gradient를 계산하는 데 사용되는 기법이 CNN과 조금 다른 양상을 보인다. RNN의 경우 step마다 사용되는 매개변수가 동일하다. 첫 번째 입력 값과 hidden state에 적용되는 행렬 W와 두 번째 입력 값과 hidden state에 적용되는 행렬 W가 같다는 의미이다.
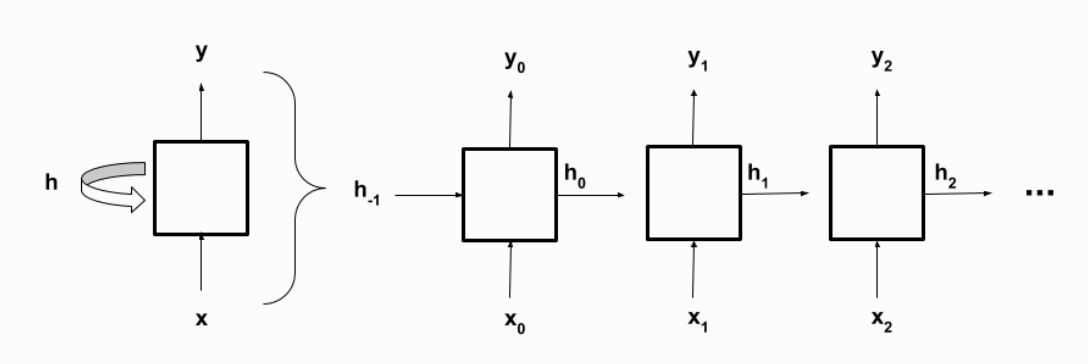
이미지의 좌측과 같은 순환적인 형태를 보이기 때문에, 역전파가 진행됨에 따라 동일한 매개변수들이 계속해서 바뀐다. 시간이 흐름에 따라 반복적으로 몇몇 매개변수에 대한 역전파가 진행된다는 의미에서 BPTT(Backpropagation through time) 기법이라 한다.
※ 역전파를 진행하며 각 step의 iteration을 마칠 때마다 gradient를 null로 초기화해야 한다. gradient 값이 누적되어 gradient의 정확성을 현저히 떨어뜨릴 수 있기 때문이다. 심지어 RNN의 경우, hidden state를 고려해야 해서 CNN보다 더 많은 시간과 메모리를 필요로하기 때문에 이와 같은 gradient 초기화 과정은 필수적이다.
수열 예측을 위한 RNN 모델
간단한 패턴을 갖는 이진 수열을 생성하고, 이 수열의 다음 값을 예측하는 모델을 구축한다.
숫자가 반복되는 간단한 패턴(ex. 0, 1, 0, 1)을 사용했다.
1. 라이브러리 임포트
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import SimpleRNN, Dense
2. 데이터 생성 및 전처리
def generate_binary_sequence(length):
# 간단한 반복 패턴 0, 1
sequence = [0, 1] * (length // 2)
return sequence
# 전체 수열 생성
seq_length = 30 # 총 수열 길이
binary_sequence = generate_binary_sequence(seq_length)
# 입력 데이터와 레이블 데이터 생성
X = []
y = []
n_steps = 4 # 한 번에 고려할 스텝 수
for i in range(len(binary_sequence) - n_steps):
X.append(binary_sequence[i:i+n_steps])
y.append(binary_sequence[i+n_steps])
# numpy 배열로 변환 및 차원 변경
X = np.array(X).reshape(len(X), n_steps, 1) # (샘플 수, 타임 스텝 수, 특성 수)
y = np.array(y)- 데이터 생성: 0과 1이 반복되는 간단한 패턴을 생성한다.
- 데이터 전처리: 입력(X)과 레이블(y)를 생성한다. 각 입력은 이전 n_steps 숫자이고, 레이블은 그 다음 숫자이다.
3. 모델 구성 및 컴파일
model = Sequential()
model.add(SimpleRNN(20, input_shape=(n_steps, 1), activation='relu'))
model.add(Dense(1, activation='sigmoid')) # 이진 분류 문제
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])- 모델 구성: SimpleRNN 레이어로 순환 신경망을 구성하고 Dense 레이어로 출력을 생성한다. 활성화 함수로 ReLU를 사용하고 출력층에는 시그모이드를 사용하여 이진 분류 문제를 해결한다.
- 모델 컴파일: 'adam' 옵티마이저와 'binary_crossentropy' 손실 함수를 사용한다.
5. 모델 훈련
model.fit(X, y, epochs=100, batch_size=5)- 모델 훈련: 모델을 수열 데이터로 훈련한다.
6. 모델 평가 및 예측
# 예측
last_sequence = np.array(binary_sequence[-n_steps:]).reshape(1, n_steps, 1)
predicted = model.predict(last_sequence)
predicted_binary = (predicted > 0.5).astype(int) # 확률을 이진 값으로 변환
print(f"Next number prediction: {predicted_binary.flatten()[0]}")- 예측: 학습된 모델을 사용하여 다음 숫자를 예측한다. 예측된 값은 확률이므로 0.5 이상인 경우 1로, 그렇지 않으면 0으로 변환한다.
'Natural Language Processing' 카테고리의 다른 글
| [NLP] Word embeddings (1) | 2024.05.04 |
|---|---|
| [NLP] 기본 언어 모델 (1) | 2024.05.03 |
| [NLP] 환경 설정 (0) | 2024.05.03 |
